A Geometric Flow for Diffeomorphisms of $\T^2$

Anthony Carapetis

(Work with Ben Andrews)


Australian National University

The idea

  • Given a diffeomorphism of a compact manifold $M$, use some geometric flow to deform it to a nicer one.
  • Potential applications: obtaining harmonic (or otherwise nice) representatives for mapping classes; retractions of ${\rm Diff}(M)$ onto smaller subgroups.
  • For today, let $M=\T^2=\R^2/\Z^2$.

The picture

domain
$u$
$\mapsto$

What flow?

  • The harmonic map heat flow $\frac{\p u}{\p t} =\Delta u := g^{ij}\nabla_i \nabla_j u$ doesn't stay inside ${\rm Diff}(M)$.
  • We study the quasilinear modification $$\tag{1}\frac{\p u}{\p t} = F(Du) \Delta u$$ with $F(Du) = (|Du|^2 + 2 \det Du)^{-1}.$

Theorem.  For any initial condition $u_0 \in {\rm Diff}(\T^2)$, there is a solution $u : [0,\infty) \to {\rm Diff}(\T^2)$ of $(1)$ with $u(x,0) = u_0(x)$, and $u$ converges smoothly to a harmonic diffeomorphism as $t\to \infty.$

Preserving Diffeomorphisms

  • One major advantage of 2nd order parabolic equations is the availability of maximum principles.
  • Since homotopy (and thus a flow solution) preserves degree, it suffices to preserve the condition that $u$ is a local diffeomorphism; i.e. that $Du$ is everywhere invertible.
  • Thus we look for some measurement of invertibility of the derivative which satisfies a maximum principle.
  • What are the natural geometric measurements?

Singular Value Decomposition

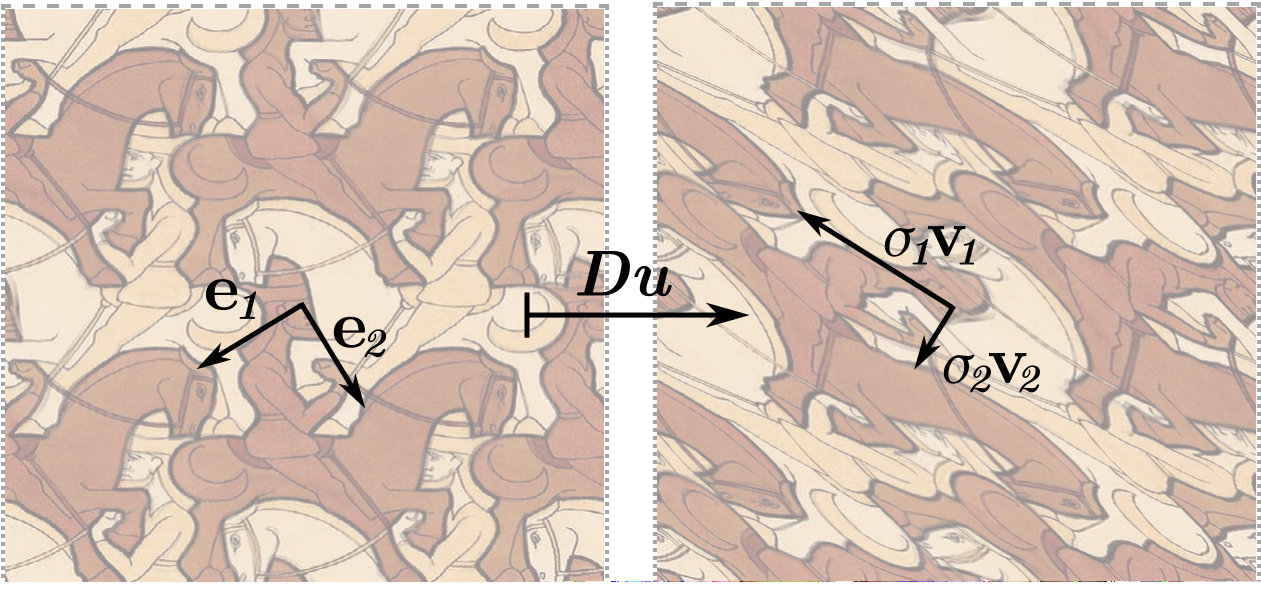SVD Illustration $Du(\v{e}_i) = \sigma_i \v v_i$ with $\sigma_i \ge 0;\;\v{e}_i, \v{v}_i$ orthonormal frames
Fun Fact: $F(Du) = (\sigma_1 + \sigma_2)^{-2}.$

SVD, the induced metric and diffeomorphisms

  • Singular values can fail to be differentiable at points where $\sigma_1 = \sigma_2$, so it's tricky to get a MP for $\sigma_{\rm min}$ alone.
  • The squared singular values $\sigma_i^2$ are the eigenvalues of the induced metric $h_{ij} = u_i^\alpha u_j^\beta (g_{\alpha \beta} \circ u)$.
  • $Du$ is invertible iff both singular values $\sigma_i$ are positive.
  • Thus preserving any inequality $h(w,w) \ge \lambda^2 |w|^2$ of symmetric bilinear forms with $\lambda \gt 0$ would preserve diffeomorphisms.

Maximum principle for $h$

  • Assume $h(\cdot,\cdot)$ has a new minimum of $\lambda^2$ over $UTM$ at $(p,w,t)$, and define $H=h(W,W)$ for $W \in \Gamma(UTM)$ extending $w$. Write $P = \p_t - F\Delta$. Then at $(p,t)$:
    • $\p_t H \lt 0, \Delta H \ge 0 \implies PH \lt 0$
    • $(\nabla_i h)(w,w) = 0$
    • $h \ge \lambda^2$ with equality at $w$
  • So we can rule out new minima by assuming the last two conditions and showing $$\sup_W P(h(W,W)) \ge 0.$$

Maximum principle for $h$

  • This reduces to $Q = (Ph)(w,w) + Q_\Gamma \ge 0$ where $$ Q_\Gamma = -2 \inf_\Gamma F\left( 2\nabla_{i} h_{kl}\Gamma_i^k w^l + (h-\lambda^2 g)_{kl}\Gamma_i^k \Gamma_i^l\right).$$ and $\Gamma^k_i = \nabla_i W^k|_{(p,t)}$.
  • Choose normal coordinates generated by $\{w = e_1, e_2\}$ and $\{v_1, v_2\}$, so we have $$Du=\left(\begin{matrix}\sigma_1 = \lambda&0 \\ 0 & \sigma_2 \end{matrix}\right), \; h = \left(\begin{matrix}\sigma_1^2&0 \\ 0 & \sigma_2^2 \end{matrix}\right)$$

Maximum principle for $h$

  • Differentiating the flow equation $Pu=0$ gives $$Ph_{ij} = -2F\left(u_{ki}^{\alpha}u_{kj}^{\alpha}+\frac{2u_{k(i}^{k}u_{j)}^{\alpha}\Delta u^{\alpha}}{\sigma_{1}+\sigma_{2}}\right).$$
  • Thus when $w=e_1 = \partial_1$ minimizes $h$ we get $$Ph(w,w) = -2F\left(u^2_{11} u^2_{11} + u^2_{12} u^2_{12} + \frac{2 \sigma_1}{\sigma_1 + \sigma_2} u^2_{12}u^1_{22}\right).$$
  • Sign is indefinite, skews towards negative! $Q_\Gamma$ has to save us.

Maximum principle for $h$

  • Minimizing the quadratic polynomial in $Q_\Gamma$ gives $$Q_\Gamma = 2F\frac{\sigma_2^2 (u^2_{11})^2 + (\sigma_1 u^1_{22} + \sigma_2 u^2_{12})^2}{\sigma_2 ^2 - \sigma_1^2}.$$
  • Combining this with $(Ph)(w,w)$ we get $$Q = \frac{2\sigma_{1}^{2}F}{\sigma_{2}^{2}-\sigma_{1}^{2}}\left(\left(u_{11}^{2}\right)^{2}+\left(u_{12}^{2}+u_{22}^{1}\right)^{2}\right)\ge0,$$ so $h\ge \lambda^2$ is preserved; i.e. $u$ remains a diffeomorphism.
  • We have some wiggle room - some other flows work.

Existence & Regularity

  • Well-known results for strongly parabolic systems provide short-time existence.
  • To get long-time existence we need bounds on all derivatives.
  • Since the equation $\p_t u = F(Du) \Delta u$ is quasilinear, a Hölder bound on $F(Du(x,t))$ along with the Schauder estimate will allow us to bootstrap all $C^{k;\alpha}$ estimates.

Sketch of Hölder Estimate

  • Let $\theta(x,t)$ be the rotation angle between the singular frames of $Du(x,t)$ and $r=F^{-1/2}=\sigma_1 + \sigma_2$. Then
    • $\p_t \theta = F \Delta \theta$, so bound on $F$ implies $\theta$ satisfies Hölder estimates; and
    • $\p_t r = F \Delta r + G(r, D \theta, Dr)$.
  • Carefully choosing constants $c_\pm,\beta_\pm$ gives super- and sub-solutions $r^{\beta_\pm} \pm c_\pm \theta^2$. Applying a weak Harnack inequality and using the $C^\alpha$ estimate for $\theta$ yields a $C^\gamma$ estimate on $r^\beta$ and thus $F$.

$\implies$ Solution exists for all time.

Long-time behaviour

  • The energy $E=\int |Du|^2$ satisfies $E'(t) = - \int F |\Delta u|^2,$ so we get smooth convergence to a harmonic limit on some sequence of times.
  • For initial data with $D^2 u$ small enough in $L^2$, the quantity $\int |D^2 u|^2$ converges exponentially to zero.
  • Combining these and interpolating we get smooth convergence as $t \to \infty$.

Thanks for listening!

Further information